Spherical geodesy

The previous chapter introduced ellipsoidal geodesy functions.

The package has also a set of spherical geodesy tools, also ported from the library developed in JavaScript by Chris Veness (see Movable Type Scripts web site and source code on GitHub).

These geodesy functions are based on calculations on a spherical earth model. Distance, bearing, destination and other functions are provided both for great circle paths and rhumb lines. All calculations use simple spherical trigonometric algorithms.

Actually the earth is slightly ellipsoidal, not spherical. However errors are typically up to 0.3% (see notes by Movable Type Scripts) when using a spherical model instead of an ellipsoidal.

🔢 Ellipsoidal vs spherical geodesy

You can try both and choose!

Ellipsoidal geodesy functions are more accurate, but spherical geodesy functions are a bit faster as the implementation is much simpler.

  // Ellipsoidal and spherical geodesy functions to calculate distances.

  final greenwich = Geographic.parseDms(lat: '51°28′40″ N', lon: '0°00′05″ W');
  final sydney = Geographic.parseDms(lat: '33.8688° S', lon: '151.2093° E');

  // How to calculate distances using ellipsoidal Vincenty, spherical
  // great-circle and spherical rhumb line methods is shown below.

  // The distance along a geodesic on the ellipsoid surface (16983.3 km).
  greenwich.vincenty().distanceTo(sydney);

  // By default the WGS84 reference ellipsoid is used but this can be changed.
  greenwich.vincenty(ellipsoid: Ellipsoid.GRS80).distanceTo(sydney);

  // The distance along a spherical great-circle path (16987.9 km).
  greenwich.spherical.distanceTo(sydney);

  // The distance along a spherical rhumb line path (17669.8 km).
  greenwich.rhumb.distanceTo(sydney);

🧐 Great circle vs rhumb line

As already mentioned for spherical geodesy the package provides two methods, calculations along great circle paths and rhumb lines.

According to Wikipedia, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere’s center point. A rhumb line or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north.

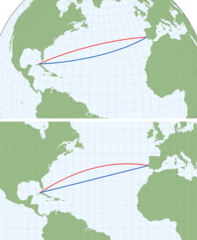
Differences between a rhumb line (blue) compared to a great-circle arc (red) as described by Wikipedia are visualized in the illustration (top: orthographic projection, bottom: Mercator projection) showing paths from Lisbon, Portugal to Havana, Cuba.

The rhumb line path is slightly longer than the path along the great circle. Rhumb lines are sometimes used in marine navigation as it’s easier to follow a constant compass bearing than adjusting bearings when following a great circle path.

🌐 Great circle paths

Examples using great circle paths (orthodromic) on a spherical earth model:

  // sample geographic positions
  final greenwich = Geographic.parseDms(lat: '51°28′40″ N', lon: '0°00′05″ W');
  final sydney = Geographic.parseDms(lat: '33.8688° S', lon: '151.2093° E');

  // decimal degrees (DD) and degrees-minutes (DM) formats
  const dd = Dms(decimals: 2);
  const dm = Dms.narrowSpace(type: DmsType.degMin, decimals: 2);

  // prints: 16987.9 km
  final distanceKm = greenwich.spherical.distanceTo(sydney) / 1000.0;
  print('${distanceKm.toStringAsFixed(1)} km');

  // prints (bearing varies along the great circle path): 60.94° -> 139.03°
  final initialBearing = greenwich.spherical.initialBearingTo(sydney);
  final finalBearing = greenwich.spherical.finalBearingTo(sydney);
  print('${dd.bearing(initialBearing)} -> ${dd.bearing(finalBearing)}');

  // prints: 51° 31.28′ N, 0° 07.50′ E
  final destPoint =
      greenwich.spherical.destinationPoint(distance: 10000, bearing: 61.0);
  print(destPoint.latLonDms(format: dm));

  // prints: 28° 33.97′ N, 104° 41.62′ E
  final midPoint = greenwich.spherical.midPointTo(sydney);
  print(midPoint.latLonDms(format: dm));

  // intermediate points along the great circle between Greenwich and Sydney
  // prints 10 intermediate geographic positions:
  // 0.0: 51° 28.67′ N, 0° 00.08′ W
  // 0.1: 56° 33.44′ N, 24° 42.13′ E
  // 0.2: 55° 50.76′ N, 52° 19.42′ E
  // 0.3: 49° 39.17′ N, 75° 34.08′ E
  // 0.4: 40° 00.39′ N, 92° 22.91′ E
  // 0.5: 28° 33.97′ N, 104° 41.62′ E
  // 0.6: 16° 14.46′ N, 114° 29.30′ E
  // 0.7: 3° 31.26′ N, 123° 05.85′ E
  // 0.8: 9° 16.56′ S, 131° 28.24′ E
  // 0.9: 21° 51.83′ S, 140° 28.86′ E
  // 1.0: 33° 52.13′ S, 151° 12.56′ E
  for (var fr = 0.0; fr < 1.0; fr += 0.1) {
    final ip = greenwich.spherical.intermediatePointTo(sydney, fraction: fr);
    print('${fr.toStringAsFixed(1)}: ${ip.latLonDms(format: dm)}');
  }

  // prints: 0° 00.00′ N, 125° 18.98′ E
  final intersection = greenwich.spherical.intersectionWith(
    bearing: 61.0,
    other: const Geographic(lat: 0.0, lon: 179.0),
    otherBearing: 270.0,
  );
  if (intersection != null) {
    print(intersection.latLonDms(format: dm));
  }

🗺️ Rhumb line paths

Examples using rhumb line paths (loxodromic) on a spherical earth model:

  // prints: 17669.8 km
  final distanceKm = greenwich.rhumb.distanceTo(sydney) / 1000.0;
  print('${distanceKm.toStringAsFixed(1)} km');

  // prints (bearing remains the same along the rhumb line): 122.49° -> 122.49°
  final initialBearing = greenwich.rhumb.initialBearingTo(sydney);
  final finalBearing = greenwich.rhumb.finalBearingTo(sydney);
  print('${dd.bearing(initialBearing)} -> ${dd.bearing(finalBearing)}');

  // prints: 51° 25.80′ N, 0° 07.26′ E
  final destPoint =
      greenwich.spherical.destinationPoint(distance: 10000, bearing: 122.0);
  print(destPoint.latLonDms(format: dm));

  // prints: 8° 48.27′ N, 80° 43.98′ E
  final midPoint = greenwich.rhumb.midPointTo(sydney);
  print(midPoint.latLonDms(format: dm));

More examples are provided in the API documentation and test cases.